$$ \newcommand{\bone}{\mathbf{1}} \newcommand{\bbeta}{\mathbf{\beta}} \newcommand{\bdelta}{\mathbf{\delta}} \newcommand{\bepsilon}{\mathbf{\epsilon}} \newcommand{\blambda}{\mathbf{\lambda}} \newcommand{\bomega}{\mathbf{\omega}} \newcommand{\bpi}{\mathbf{\pi}} \newcommand{\bphi}{\mathbf{\phi}} \newcommand{\bvphi}{\mathbf{\varphi}} \newcommand{\bpsi}{\mathbf{\psi}} \newcommand{\bsigma}{\mathbf{\sigma}} \newcommand{\btheta}{\mathbf{\theta}} \newcommand{\btau}{\mathbf{\tau}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\boldf}{\mathbf{f}} \newcommand{\bg}{\mathbf{g}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bell}{\mathbf{\ell}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{o}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bW}{\mathbf{W}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calD}{\mathcal{D}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calI}{\mathcal{I}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calQ}{\mathcal{Q}} \newcommand{\calR}{\mathcal{R}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\calY}{\mathcal{Y}} \newcommand{\calZ}{\mathcal{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\F}{\mathbb{F}} \newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\nnz}[1]{\mbox{nnz}(#1)} \newcommand{\dotprod}[2]{\langle #1, #2 \rangle} \newcommand{\ignore}[1]{} \let\Pr\relax \DeclareMathOperator*{\Pr}{\mathbf{Pr}} \newcommand{\E}{\mathbb{E}} \DeclareMathOperator*{\Ex}{\mathbf{E}} \DeclareMathOperator*{\Var}{\mathbf{Var}} \DeclareMathOperator*{\Cov}{\mathbf{Cov}} \DeclareMathOperator*{\stddev}{\mathbf{stddev}} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\codim}{codim} \DeclareMathOperator{\diag}{diag} \newcommand{\PTIME}{\mathsf{P}} \newcommand{\LOGSPACE}{\mathsf{L}} \newcommand{\ZPP}{\mathsf{ZPP}} \newcommand{\RP}{\mathsf{RP}} \newcommand{\BPP}{\mathsf{BPP}} \newcommand{\P}{\mathsf{P}} \newcommand{\NP}{\mathsf{NP}} \newcommand{\TC}{\mathsf{TC}} \newcommand{\AC}{\mathsf{AC}} \newcommand{\SC}{\mathsf{SC}} \newcommand{\SZK}{\mathsf{SZK}} \newcommand{\AM}{\mathsf{AM}} \newcommand{\IP}{\mathsf{IP}} \newcommand{\PSPACE}{\mathsf{PSPACE}} \newcommand{\EXP}{\mathsf{EXP}} \newcommand{\MIP}{\mathsf{MIP}} \newcommand{\NEXP}{\mathsf{NEXP}} \newcommand{\BQP}{\mathsf{BQP}} \newcommand{\distP}{\mathsf{dist\textbf{P}}} \newcommand{\distNP}{\mathsf{dist\textbf{NP}}} \newcommand{\eps}{\epsilon} \newcommand{\lam}{\lambda} \newcommand{\dleta}{\delta} \newcommand{\simga}{\sigma} \newcommand{\vphi}{\varphi} \newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\wt}[1]{\widetilde{#1}} \newcommand{\wh}[1]{\widehat{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\ot}{\otimes} \newcommand{\zo}{\{0,1\}} \newcommand{\co}{:} %\newcommand{\co}{\colon} \newcommand{\bdry}{\partial} \newcommand{\grad}{\nabla} \newcommand{\transp}{^\intercal} \newcommand{\inv}{^{-1}} \newcommand{\symmdiff}{\triangle} \newcommand{\symdiff}{\symmdiff} \newcommand{\half}{\tfrac{1}{2}} \newcommand{\bbone}{\mathbbm 1} \newcommand{\Id}{\bbone} \newcommand{\SAT}{\mathsf{SAT}} \newcommand{\bcalG}{\boldsymbol{\calG}} \newcommand{\calbG}{\bcalG} \newcommand{\bcalX}{\boldsymbol{\calX}} \newcommand{\calbX}{\bcalX} \newcommand{\bcalY}{\boldsymbol{\calY}} \newcommand{\calbY}{\bcalY} \newcommand{\bcalZ}{\boldsymbol{\calZ}} \newcommand{\calbZ}{\bcalZ} $$

2020

  1. Extracting Training Data from Large Language Models

    Nicholas Carlini, Florian Tramer, Eric Wallace, and 9 more authors
    Dec 2020
    arXiv Bib PDF

    Paper Abstract

    It has become common to publish large (billion parameter) language models that have been trained on private datasets. This paper demonstrates that in such settings, an adversary can perform a training data extraction attack to recover individual training examples by querying the language model. We demonstrate our attack on GPT-2, a language model trained on scrapes of the public Internet, and are able to extract hundreds of verbatim text sequences from the model’s training data. These extracted examples include (public) personally identifiable information (names, phone numbers, and email addresses), IRC conversations, code, and 128-bit UUIDs. Our attack is possible even though each of the above sequences are included in just one document in the training data. We comprehensively evaluate our extraction attack to understand the factors that contribute to its success. Worryingly, we find that larger models are more vulnerable than smaller models. We conclude by drawing lessons and discussing possible safeguards for training large language models.

Three Important Things

1. Training Data Extraction Attack

In this paper, the authors come up with and investigate the efficacy of a training data extraction attack on large language models. To mitigate the potential harms of the study, they performed this on GPT-2, where both the training dataset and models are already public. They used the largest GPT-2 model with 1.5 billion parameters.

An example of personally identifiable information that they managed to extract is given below (with permission from the individual affected):

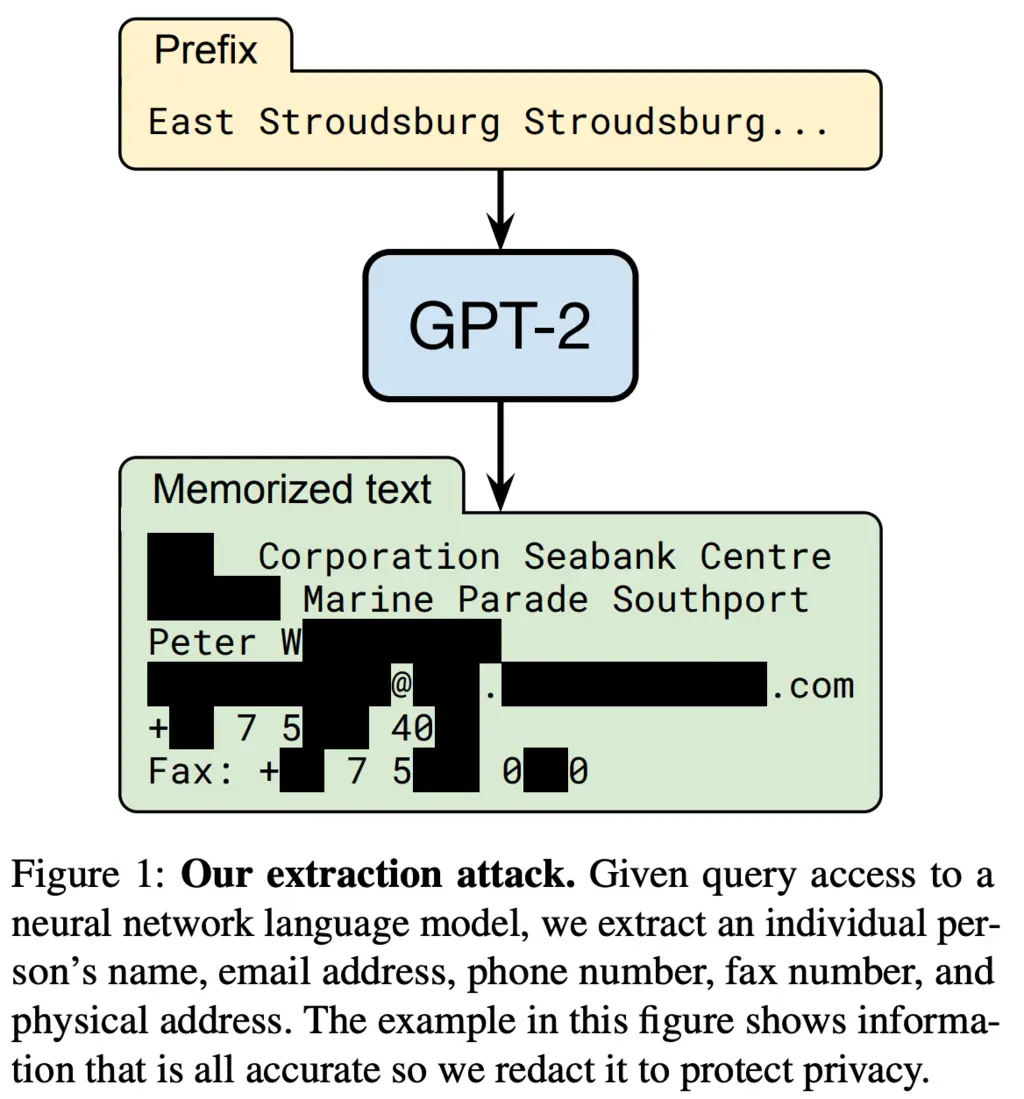
The table below shows the types of memorized content that they were able to recover:

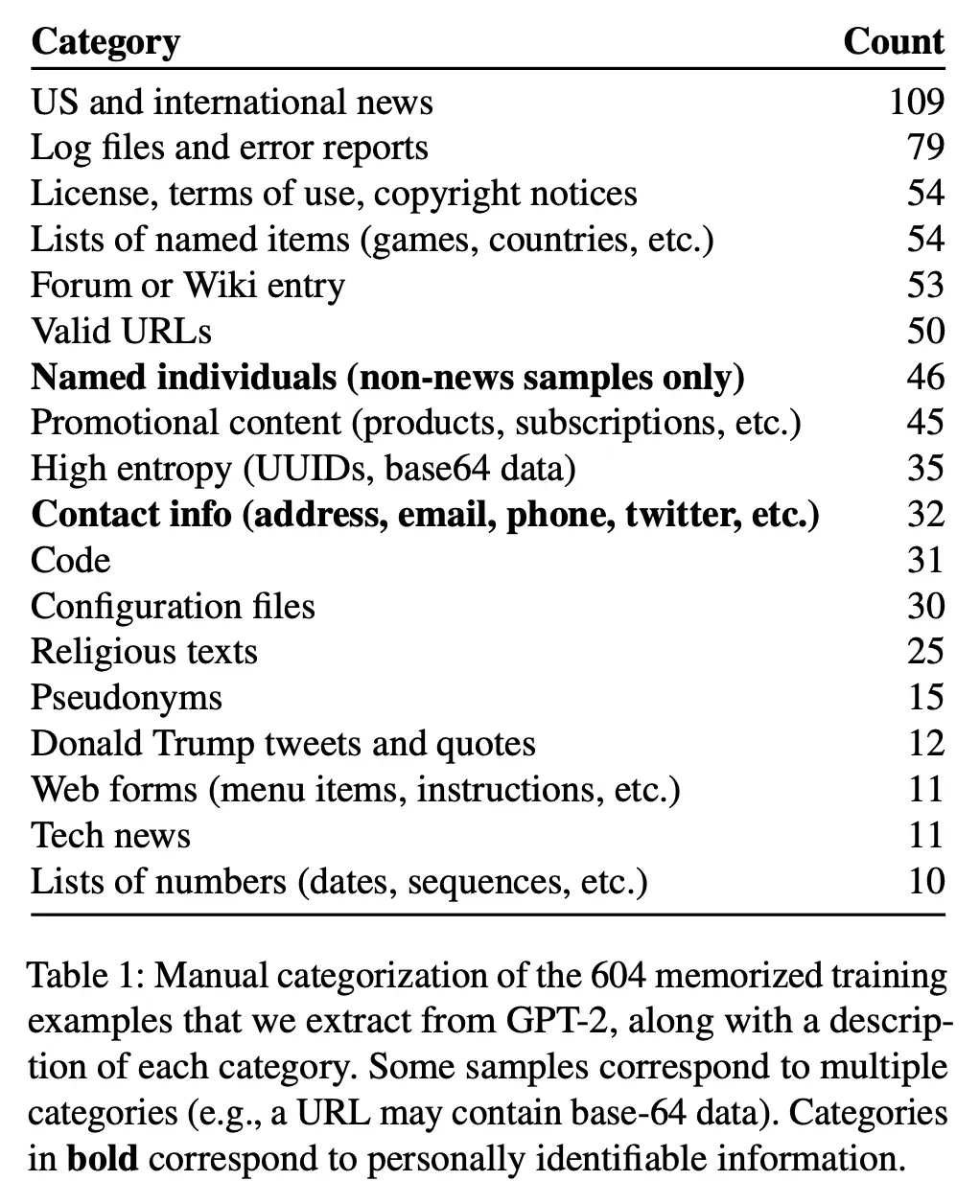
Since it is possible that many common text phrases will be memorized by the language model (such as the MIT license), the authors are concerned only about uncovering eidetic memorization. This is data that is memorized despite only appearing a very small number of times.

Formally, they define \(k\)-eidetic memorization for a string \(s\) as being able to recover \(s\) from the language model using a “reasonable” prompt, when it only appears at most \(k\) times in the training dataset. There is some nuance here about whether a prompt is reasonable as there are pathological corner cases where you could simply ask the prompt to repeat a string back to you. This was not mentioned in the paper, but I believe a reasonable working definition could be that there is information gain (in a Shannon entropy manner) when I see the result, conditioned on the prompt.

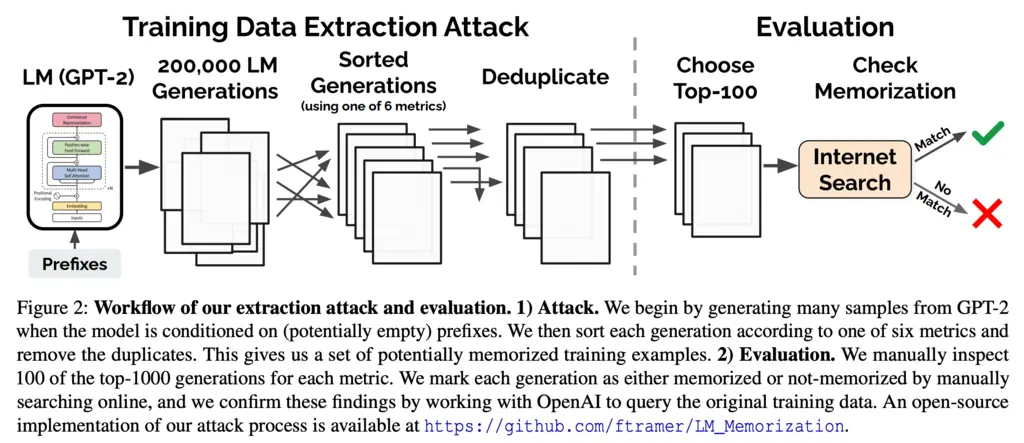
The high-level workflow of their attack is as follows.

  1. They provide prompts (potentially just the empty start-of-sentence token) to the GPT-2 language model, and auto-regressively sample from it
  2. Use one of 6 metrics to determine the likelihood that each of the generations contains memorized content. These will be discussed later.
  3. The generated texts are de-duplicated
  4. The top 100 generations (according to the metric) are chosen
  5. The researchers manually verified whether the generations are indeed memorized by an internet search, with confirmation with OpenAI (who developed GPT-2)

2. Text Generation Schemes

The authors initially faced the problem of having a low diversity of outputs when just performing top-\(n\) sampling autoregressively on an empty prompt. To increase the precision and recall of generated text that corresponds to eidetic memorization, they found two techniques that helped:

  1. Sampling with a Decaying Temperature: Borrowing ideas from simulated tempering, they initially start sampling with a higher temperature which then decays throughout the generation process. Decaying the temperature is necessary to eventually extract high-confidence sequences.

  2. Conditioning on Internet text: The authors curated a dataset that was a cleaned subset of the Common Crawl, and used short samples from this dataset as prompts. They found that using Internet-sourced text as prompts helped to elicit a larger diversity of responses from GPT-2, which was also trained on Internet data.

3. Membership Inference

After generating 200,000 samples, it is very much infeasible to try to evaluate them all by hand to determine whether they were memorized, and hence the authors used different heuristics as metrics to determine the likelihood that a piece of generated sample was eidetically memorized.

  1. Comparing to other neural language models: they compared the perplexity of the output from the largest 1.5 billion GPT-2 XL model against its smaller counterparts: Small (117M parameters) and Medium (345M parameters). If a piece of output was not surprising to the XL model but was surprising to either the Small or Medium model, then it likely indicates that the output was \(k\)-eidetic memorized and is not a product of general natural language.
  2. Comparing to zlib compression: a common failure mode was the propensity for the text to spit out repetitive text which has low perplexity, despite this being very unnatural in real life, such as the repeated text “I love you. I love you. I love you…”. To catch this case, the authors applied zlib compression on the output, and used the ratio of perplexity to zlib compression entropy as a metric.
  3. Comparing to lowercased text: they measured the perplexity of both the original output, and when it is completely lowercased. If the lowercased output has much higher perplexity (indicating the casing was important), then it hints that it was likely memorized.
  4. Perplexity on sliding window: In some cases only a part of the output has low perplexity and contains memorized text, while other parts could have low likelihood. This is especially so if simulated tempering was used. As such, the minimum perplexity averaged over a sliding window of 50 tokens was used.

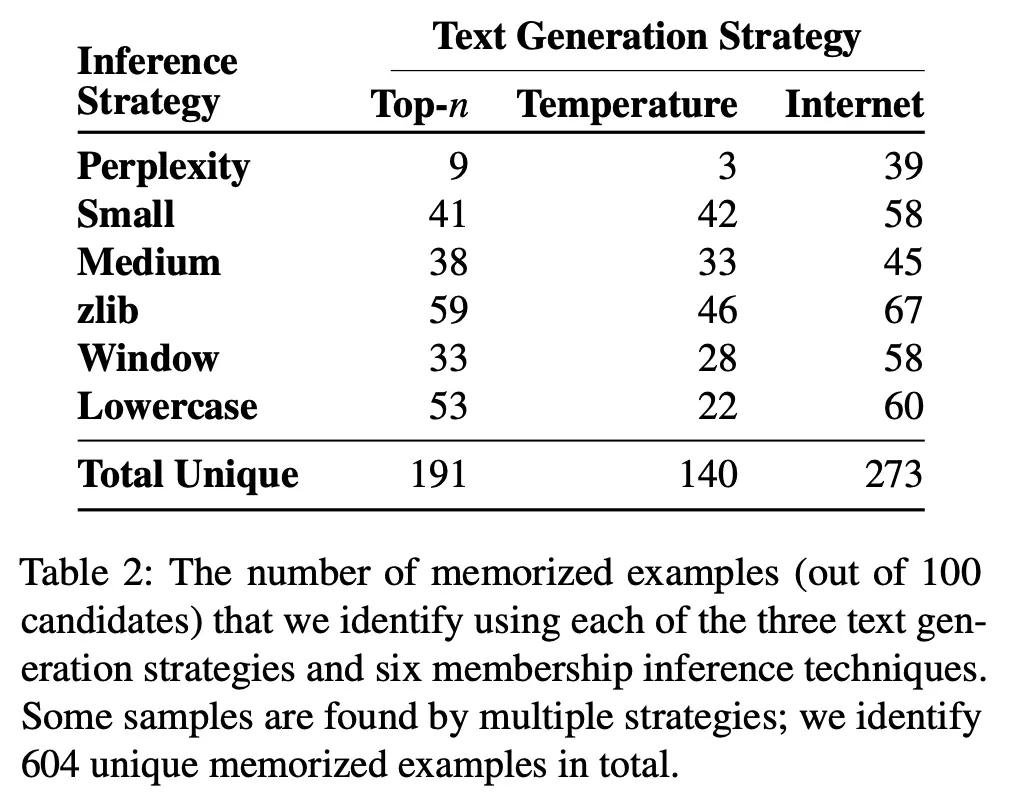
The number of memorized samples recovered using each of these metrics and text generation strategies are given below:

Most Glaring Deficiency

The different metrics for membership inference are orthogonal in some sense that they each have different strengths. I feel that the authors could have experimented with combining the metrics, weighted in some appropriate manner, to obtain even higher rates of recovering eidetically memorized content.

Conclusions for Future Work

The results of this paper are an understatement of the true extent to which training data can be recovered from black-box querying of large language models. As models get larger, this is only going to become an even bigger issue.

This also shows that concerns from companies using foundation models for their internal use about not having their confidential data trained on are extremely valid, and per-organization fine-tuned models to avoid information leakage may be fundamentally unavoidable unless there is a way to train in a privacy-preserving manner without incurring a huge computational tax.

Written 2023