$$ \newcommand{\bone}{\mathbf{1}} \newcommand{\bbeta}{\mathbf{\beta}} \newcommand{\bdelta}{\mathbf{\delta}} \newcommand{\bepsilon}{\mathbf{\epsilon}} \newcommand{\blambda}{\mathbf{\lambda}} \newcommand{\bomega}{\mathbf{\omega}} \newcommand{\bpi}{\mathbf{\pi}} \newcommand{\bphi}{\mathbf{\phi}} \newcommand{\bvphi}{\mathbf{\varphi}} \newcommand{\bpsi}{\mathbf{\psi}} \newcommand{\bsigma}{\mathbf{\sigma}} \newcommand{\btheta}{\mathbf{\theta}} \newcommand{\btau}{\mathbf{\tau}} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\boldf}{\mathbf{f}} \newcommand{\bg}{\mathbf{g}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bell}{\mathbf{\ell}} \newcommand{\bm}{\mathbf{m}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{o}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bt}{\mathbf{t}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bA}{\mathbf{A}} \newcommand{\bB}{\mathbf{B}} \newcommand{\bC}{\mathbf{C}} \newcommand{\bD}{\mathbf{D}} \newcommand{\bE}{\mathbf{E}} \newcommand{\bF}{\mathbf{F}} \newcommand{\bG}{\mathbf{G}} \newcommand{\bH}{\mathbf{H}} \newcommand{\bI}{\mathbf{I}} \newcommand{\bJ}{\mathbf{J}} \newcommand{\bK}{\mathbf{K}} \newcommand{\bL}{\mathbf{L}} \newcommand{\bM}{\mathbf{M}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bP}{\mathbf{P}} \newcommand{\bQ}{\mathbf{Q}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bS}{\mathbf{S}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bU}{\mathbf{U}} \newcommand{\bV}{\mathbf{V}} \newcommand{\bW}{\mathbf{W}} \newcommand{\bX}{\mathbf{X}} \newcommand{\bY}{\mathbf{Y}} \newcommand{\bZ}{\mathbf{Z}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calD}{\mathcal{D}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calI}{\mathcal{I}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calQ}{\mathcal{Q}} \newcommand{\calR}{\mathcal{R}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\calY}{\mathcal{Y}} \newcommand{\calZ}{\mathcal{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Z}{\mathbb{Z}} \newcommand{\F}{\mathbb{F}} \newcommand{\Q}{\mathbb{Q}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\nnz}[1]{\mbox{nnz}(#1)} \newcommand{\dotprod}[2]{\langle #1, #2 \rangle} \newcommand{\ignore}[1]{} \let\Pr\relax \DeclareMathOperator*{\Pr}{\mathbf{Pr}} \newcommand{\E}{\mathbb{E}} \DeclareMathOperator*{\Ex}{\mathbf{E}} \DeclareMathOperator*{\Var}{\mathbf{Var}} \DeclareMathOperator*{\Cov}{\mathbf{Cov}} \DeclareMathOperator*{\stddev}{\mathbf{stddev}} \DeclareMathOperator*{\avg}{avg} \DeclareMathOperator{\poly}{poly} \DeclareMathOperator{\polylog}{polylog} \DeclareMathOperator{\size}{size} \DeclareMathOperator{\sgn}{sgn} \DeclareMathOperator{\dist}{dist} \DeclareMathOperator{\vol}{vol} \DeclareMathOperator{\spn}{span} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\Tr}{Tr} \DeclareMathOperator{\codim}{codim} \DeclareMathOperator{\diag}{diag} \newcommand{\PTIME}{\mathsf{P}} \newcommand{\LOGSPACE}{\mathsf{L}} \newcommand{\ZPP}{\mathsf{ZPP}} \newcommand{\RP}{\mathsf{RP}} \newcommand{\BPP}{\mathsf{BPP}} \newcommand{\P}{\mathsf{P}} \newcommand{\NP}{\mathsf{NP}} \newcommand{\TC}{\mathsf{TC}} \newcommand{\AC}{\mathsf{AC}} \newcommand{\SC}{\mathsf{SC}} \newcommand{\SZK}{\mathsf{SZK}} \newcommand{\AM}{\mathsf{AM}} \newcommand{\IP}{\mathsf{IP}} \newcommand{\PSPACE}{\mathsf{PSPACE}} \newcommand{\EXP}{\mathsf{EXP}} \newcommand{\MIP}{\mathsf{MIP}} \newcommand{\NEXP}{\mathsf{NEXP}} \newcommand{\BQP}{\mathsf{BQP}} \newcommand{\distP}{\mathsf{dist\textbf{P}}} \newcommand{\distNP}{\mathsf{dist\textbf{NP}}} \newcommand{\eps}{\epsilon} \newcommand{\lam}{\lambda} \newcommand{\dleta}{\delta} \newcommand{\simga}{\sigma} \newcommand{\vphi}{\varphi} \newcommand{\la}{\langle} \newcommand{\ra}{\rangle} \newcommand{\wt}[1]{\widetilde{#1}} \newcommand{\wh}[1]{\widehat{#1}} \newcommand{\ol}[1]{\overline{#1}} \newcommand{\ul}[1]{\underline{#1}} \newcommand{\ot}{\otimes} \newcommand{\zo}{\{0,1\}} \newcommand{\co}{:} %\newcommand{\co}{\colon} \newcommand{\bdry}{\partial} \newcommand{\grad}{\nabla} \newcommand{\transp}{^\intercal} \newcommand{\inv}{^{-1}} \newcommand{\symmdiff}{\triangle} \newcommand{\symdiff}{\symmdiff} \newcommand{\half}{\tfrac{1}{2}} \newcommand{\bbone}{\mathbbm 1} \newcommand{\Id}{\bbone} \newcommand{\SAT}{\mathsf{SAT}} \newcommand{\bcalG}{\boldsymbol{\calG}} \newcommand{\calbG}{\bcalG} \newcommand{\bcalX}{\boldsymbol{\calX}} \newcommand{\calbX}{\bcalX} \newcommand{\bcalY}{\boldsymbol{\calY}} \newcommand{\calbY}{\bcalY} \newcommand{\bcalZ}{\boldsymbol{\calZ}} \newcommand{\calbZ}{\bcalZ} $$

2019

  1. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer

    Colin Raffel, Noam Shazeer, Adam Roberts, and 6 more authors
    Oct 2019
    arXiv Bib PDF

    Paper Abstract

    Transfer learning, where a model is first pre-trained on a data-rich task before being fine-tuned on a downstream task, has emerged as a powerful technique in natural language processing (NLP). The effectiveness of transfer learning has given rise to a diversity of approaches, methodology, and practice. In this paper, we explore the landscape of transfer learning techniques for NLP by introducing a unified framework that converts all text-based language problems into a text-to-text format. Our systematic study compares pre-training objectives, architectures, unlabeled data sets, transfer approaches, and other factors on dozens of language understanding tasks. By combining the insights from our exploration with scale and our new “Colossal Clean Crawled Corpus”, we achieve state-of-the-art results on many benchmarks covering summarization, question answering, text classification, and more. To facilitate future work on transfer learning for NLP, we release our data set, pre-trained models, and code.

Three Important Things

The authors state that the goal of the paper is not to introduce any novel ideas, but rather to push the limits of the current known architecture and see what results can be achieved.

1. Text-to-Text Transfer Transformer (T5)

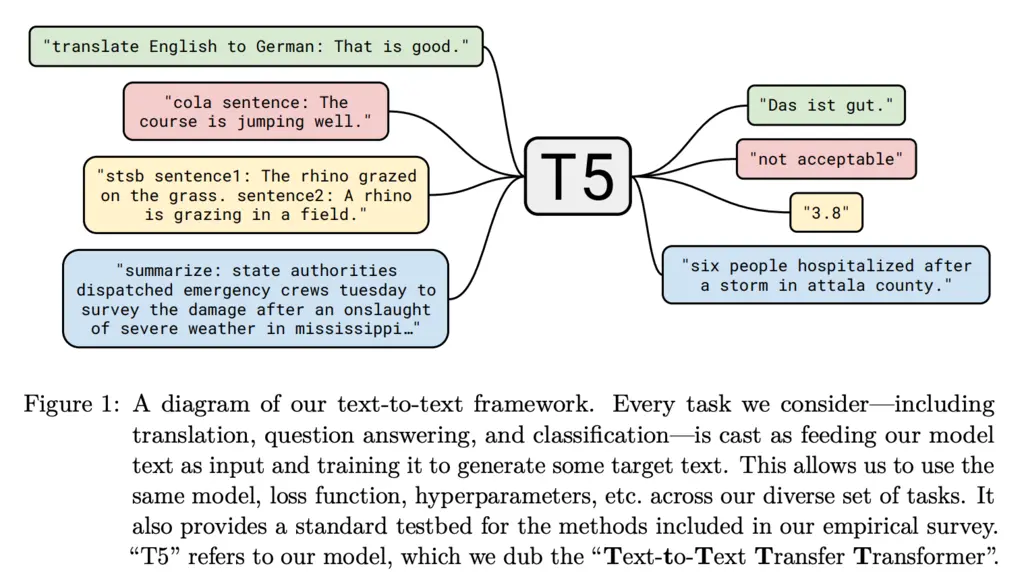
The Text-to-Text Transfer Transformer (T5) model has an encoder-decoder architecture. The author takes the view that all problems can be viewed as a text-to-text problem, and therefore this architecture can generalize to all NLP tasks.

The encoder has a “fully-visible” attention mask, meaning that the attention mechanism can attend to any position in the input. On the other hand, the decoder has a “causal” attention mask, and can only attend to tokens \(j < i\) when it is trying to compute the token at position \(i\), to prevent it from seeing the future inputs which would otherwise trivialize the training process.

The decoder produces the output in an autoregressive manner, meaning that it produces one output token at a time, and then concatenates this output to the input and repeats the process until the end of sequence token is output.

2. Prefix LM

While the best-performing T5 variant has an encoder-decoder architecture (which is the standard architecture T5 would refer to), the authors also experimented with and performed comparisons against the language model and prefix LM architectures.

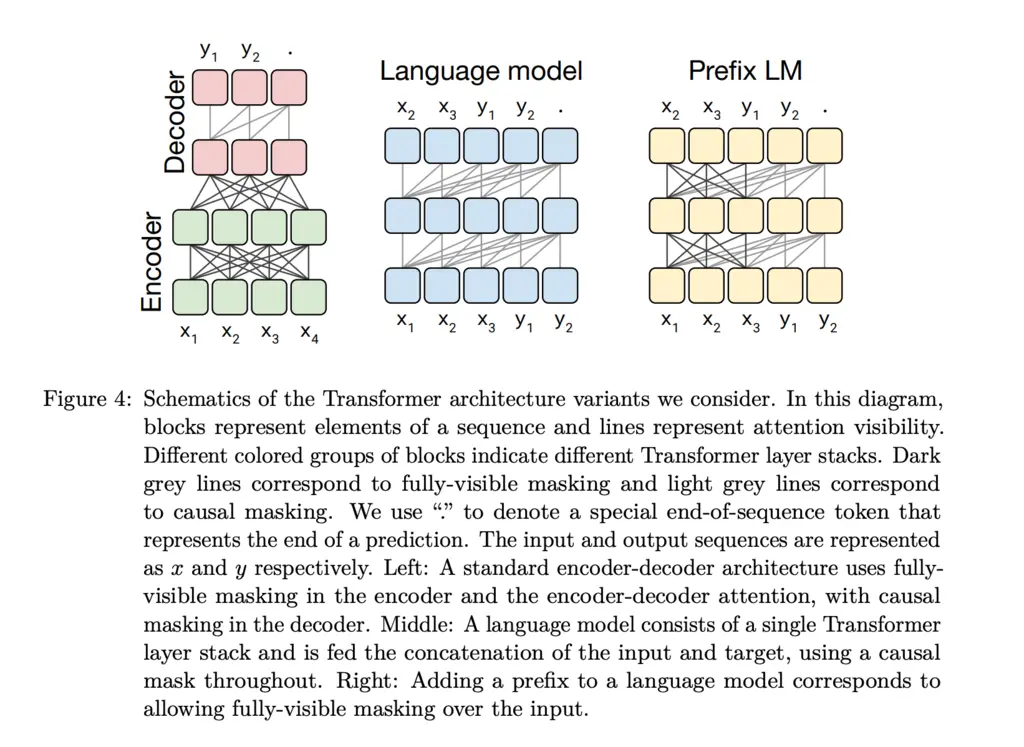
The goal of the language model architecture is to predict token \(i+1\), given all tokens up to \(i\). A major downside of this is that the model’s representation of the \(j\)th entry of the input can only depend on all tokens less than \(j\).

However, for text-to-text tasks, it could be possible that there is a lot of useful context on the right of \(j\) which is still in the input prompt that is relevant. For instance, for English to German translation, if the input prompt is translate English to German: That is good. target: , then it makes sense for the tokens at the start to also be able to attend to future tokens in the prompt.

The prefix LM architecture addresses this limitation by allowing for fully-visible masking in the prefix portion of the input, and therefore the representation of all tokens can attend to every other token in the input.

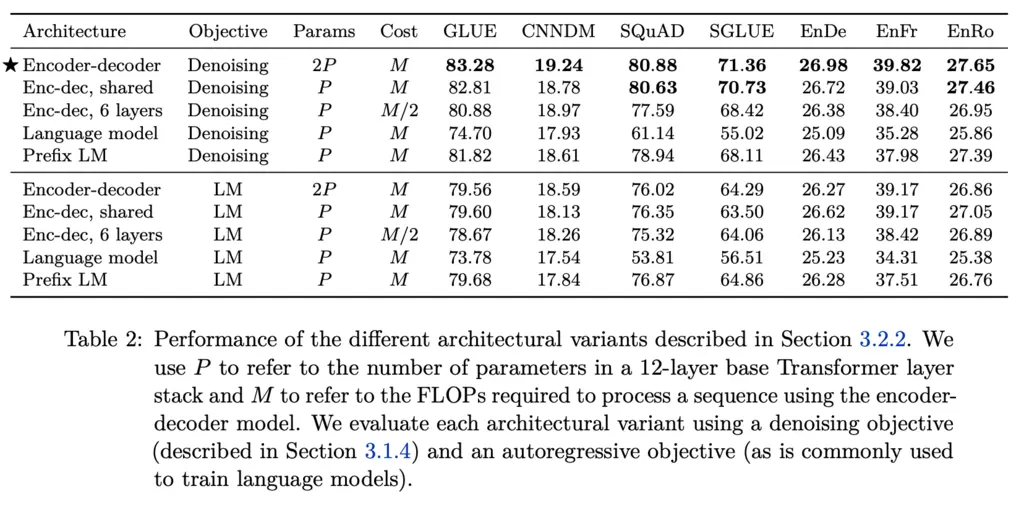
The following table shows the results of comparisons between the three architectures, with the encoder-decoder performing the best, and the language model the worst.

3. Colossal Clean Crawled Corpus

The Common Crawl is a dataset of text data scraped from the web, with around 20TB of data extracted each month. However, most of the text scraped is not natural language, and is instead web boilerplate code, error messages, gibberish, etc.

The authors cleaned up the Common Crawl to obtain the Colossal Clean Crawled Corpus (C4), by using the following heuristics:

  • Keeping only text terminated by punctuation
  • Discard pages with < 5 sentences
  • Keeping lines with at least 3 words
  • Discarding pages with offensive words
  • Removing any lines containing the word Javascript
  • Discarding any pages with “lorem ipsum” text
  • Removing pages containing a curly bracket {, as it usually indicates code
  • Deduplicating the data by removing any three-sentence span that occurs in the dataset more than once, to just having it show up once

The T5 transformer was then trained on C4 for \(2^{19} = 524,288\) steps with a max sequence length of 512, and a batch size of 128 sequences.

Most Glaring Deficiency

The method used to clean the C4 corpus feels somewhat arbitrary and perhaps still very much incomplete. Due to the importance of data in the performance of the model, it would have also been helpful to have trained on the Common Crawl as well to perform an ablation study on whether C4 resulted in better performance.

Conclusions for Future Work

The text-to-text approach for modeling language tasks is a promising avenue to generalize task-specific architectures, and could become a future default approach due to its simplicity and generalizability.

The authors also found that pushing the limits of the architecture by a very large 11-billion parameter model resulted in state-of-the-art performance across many tasks, showing that scale can result in performance gains.

Written 2023