Evaluation metrics of Object Tracking Algorithms

Detection Metrics

• Mean Square Error: x, y, w, h
• L1-Loss
• IoU: Generally good for small target, Normalized [0 -> 1].

Multiple Object Detection

• Hungarian Matching (a.k.a. Bipartite Matching)

  • maximize over all IoU
  • 1 to 1 match
  • Throw away matches with IoU < 0.5.
  • Remaining Matches = True Positives (TP)
  • Some predictions are not matched to anything (FP)
  • Some ground truth objects are not matched to anything (FN)
    
  • Problem with hungarian matching: Unstability i.e. object ID might be switched during occulusion.

• Detection Accuracy (DetA)

  \[\frac{TP}{TP + FP + FN}\]
  • Depends only on current frame (not the video sequence)
  • Depends on Hungarian matching
  • Depends on IoU threshold (0.5)
  • Good way since it pensalizes you for missing objects, detecting same object twice, or objects that are not there or inaccurately.

Multiple Object Tracking Benchmarking (MOT)

MOT17 Challenge

• Ground truth
  • Set of frames of a video sequence
  • For each frame - a set of GT objects
  • Bounding box - x, y, w, h
  • Object id - gtld
• Prediction
  • For each frame - a set of predictions
  • Bounding box - x, y, w, h
  • trackld
• Identity Switch: Occurs if same GT object us detected with different trackID. It is sovled by a modified version of Hungarian Match i.e. Sticky Hungarian Matching.
• Sticky Hungarian Matching
  • Similarity = IOU + 1000 * but if IoU < 0.5 then similarity is = O
  • Matching is done minimising new score.

So Multiple Object Tracking Accuracy (MOTA) is defined as

here (IDSW) is Identity Switch and (gtDet) is Ground Truth Detection.

• It is dependent on Sticky Hungarian Matching, current & previous frame and $IoU$ threshold (0.5).

Problems with MOTA

• IDSW contribute ~1% to metric

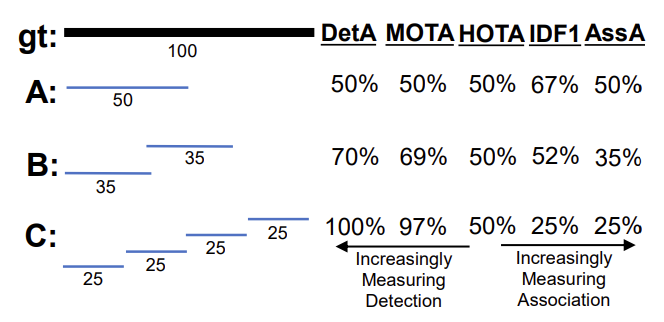
</div>

Source: HOTA Paper.. A simple tracking example highlighting one of the main differences between evaluation metrics. Three different trackers are shown in order of increasing detection accuracy and decreasing association accuracy. MOTA and IDF1 overemphasize the effect of accurate detection and association respectively. HOTA balances both of these by being an explicit combination of a detection score DetA and an association score AssA.

• Does not take detection accuracy into account (beyond 0.5 IoU)
• So researchers sometimes prefer Multiple Object Tracking Precision (MOTP)
  • \[MOTP = \frac{1}{|TP|}\sum_{TP} IoU\]
• but then we have a different problem of having two metrics i.e. MOTA for object detection and MOTP for actually evaluating which trade off we want to take between tracking and detection accuracy.

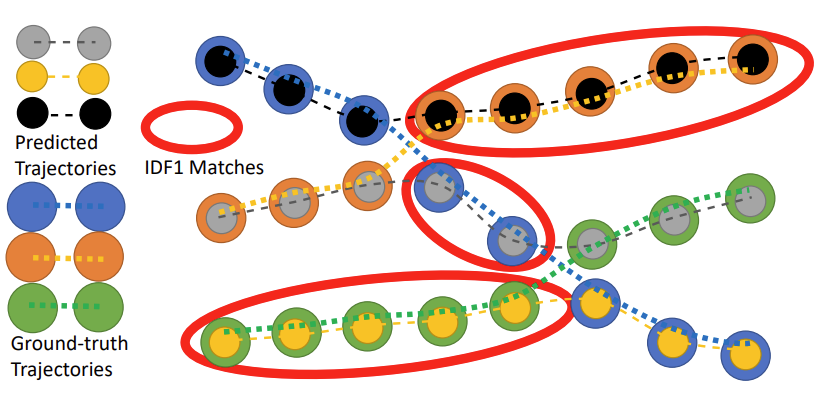
• In the above tracking example which shows how the single best trajectory matching, as performed by IDF1, can result in unintuitive matches between trajectories.

IDF1

• IDF1 in context of object tracking is slighlty different from the conventional IDF (Inverse Document Frequency) component of the TF-IDF (Term Frequency-Inverse Document Frequency) weighting scheme.

• Unlike traditional metrics that focus on frame-level accuracy, IDF1 takes into account the entire identity of objects over time, making it particularly valuable for assessing how well a tracking algorithm maintains the identity of objects across multiple frames.

• The IDF1 score is defined as the harmonic mean of the Identification Precision (IDP) and Identification Recall (IDR). These two metrics are computed as follows:

  • Identification Precision (IDP): The proportion of correctly identified detections (i.e., the correct matches of tracked objects to ground truth objects) relative to the total number of detections made by the tracker.

  • Identification Recall (IDR): The proportion of correctly identified ground truth objects relative to the total number of ground truth objects.

HOTA